Некоммерческие приложения
Дискретная математика
https://play.google.com/store/apps/details?id=com.coin.discrmath
Справочник по дискретной математике: булевые функции с возможностью решения.
Дискретная математика (дискретный анализ) занимается изучением финитных (конечных) свойств объектов, которые возникают как в различных разделах математики, так и в ее технических приложениях. Под конечными свойствами понимаются их ограниченность или перечислимость. Важными отличиями разделов дискретной математики от классических разделов непрерывной математики являются отсутствие понятия непрерывности и предела последовательности. То, что в разделах дискретной математики рассматриваются конечные свойства объектов, совсем не означает, что при исследовании не встречаются бесконечные совокупности объектов или их конфигураций, однако, как правило, эти бесконечности являются счетными. В то время как в непрерывной математике бесконечности, как правило, континуальные. Булевы функции (функции алгебры логики) описывают логику работы цифровых устройств, называемых комбинационными схемами.

Словодел
https://play.google.com/store/apps/details?id=com.coin.words
Собирайте слова - СУЩЕСТВИТЕЛЬНЫЕ из трех букв или более, используя кубики, которые падают с верхней части игрового поля. Слова могут быть построены по горизонтали или вертикали и могут пересекаться между собой. Каждый раз при получении нового уровня игровое поле очищается, а скорость падения кубика увеличивается. Если игроку удастся собрать красное слово из верхней части экрана, игровое поле очистится от всех кубиков, и игрок будет получит большой бонус. При заполнении игрового поля кубиками игра заканчивается. Периодически вместо кубиков с буквами падают знак вопроса, ластик, бомба или подарок.Знак вопроса - случайная буква, ластик убирает только одну букву на которую упадет, бомба "взрывает" поле из окружающих ее кубиков, а подарок - это именно та буква, что не хватает для составления слова!
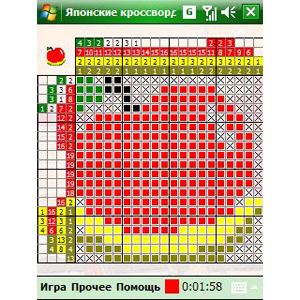
Nonogram - Японские кроссворды
Разгадывание кроссвордов - это отличный способ скоротать время и прекрасное средство для повышения эрудиции, сообразительности, расширения кругозора, тренировки памяти и логического мышления. В базе 35 кроссвордов,для добавления новых достаточно скинуть в каталог с игрой BMP 16ти цветный - программка сама превратит его в кроссворд.Есть проверка на решаемость чернобелых кроссвордов.
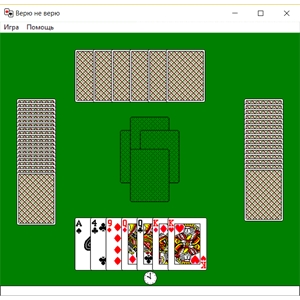
Карточная игра Верю не Верю
Данная игра представляет собой игру, на которой может быть основаны с десяток, а то и более игр. Основа игры это ситуация, когда один игрок кладет карты в закрытом виде, а другой игрок либо верит, либо не верит, тогда в этом случае вскрываются карты и проверяется правильность хода. Если карты положены правильно. то ход засчитывается в пользу ходящего, если неправильно, то ход в пользу другого не ходящего игрока, иногда бывает наоборот.
Цель игры: первым избавиться от всех своих карт. Правила игры. Первый сдатчик в игре определяется жребием, в следующих играх игроки сдают карты по очереди. Колода тщательно тасуется, снимается и раздается поровну между всеми игроками. Первый ход принадлежит игроку, который сидит слева от сдатчика. Игрок выкладывает на стол одну или несколько карт в закрытом виде, после чего называет их достоинство. Например, две восьмерки или девятка. Следующий игрок по часовой стрелке должен положить карту или карты на одно значение меньше и назвать их достоинство. Если положенные карты двойки, то на них кладутся тузы. Так игроки играют по кругу. В том случае, если игрок ошибется и положит не те карты, которые необходимо класть, то все карты со стола он забирает себе. Любой игрок имеет право сказать "сомневаюсь", "не верю", "обман", "фигня" или "мошенничество", если он не поверит игроку, который выложил карты. Если карты положены неверно, то игрок выложивший их, забирает себе все карты со стола. Если ошибся тот, кто сомневался, то он забирает себе все карты. Таким образом, игра продолжается до тех пор, пока у одного из игроков не закончатся карты. Этот игрок становится победителем.
Есть вопросы? Закажите бесплатную консультацию!
Мы свяжемся с Вами в течение 5 минут